Differential Growth

Differential Growth Curve (Grasshopper Example)
This example demonstrates how to create an animating 2D differential growth algorithm using the Anemone plugin for Grasshopper. Usually this type of algorithm requires knowledge of a coding language or the use of external plugins such as Parakeet, however we will recreate this algorithm with the Anemone looping plugin and simple grasshopper components only.
This example is available to download below for all Premium members of The Different Design.
Not a member? Sign up today!
The grasshopper example:
This example uses a basic separation algorithm that moves points away from one another, similar to the types of behaviours commonly found in Craig Reynold’s Boids simulations. In grasshopper, a collection of closest points are found, and are then culled based on distance to the current point. A vector is then created to move points away from one another to avoid collisions. To simulate growth in the algorithm, a behaviour is implemented into the end of the algorithm that inserts a new control point in the curve whenever two points have separated by a large distance.
These behaviours are then simulated in a controlled loop using the Anemone plugin for Grasshopper, and this repeating process allows for the generation organic growth of a curve, without ever creating collisions between points.
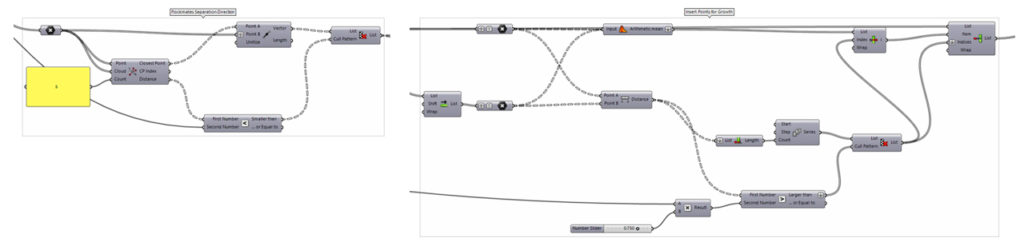
Snippets of the final algorithm showing the separation behaviour and point insertion
Producing different iterations:
The algorithm is capable of producing a number of variations each time it the simulation is run. The form of the starting curve has a significant effect on the shape of the final pattern produced (see iterations below). The separation distance between points controls the density and complexity of the curve, but can have an adverse effect on the performance of the algorithm.
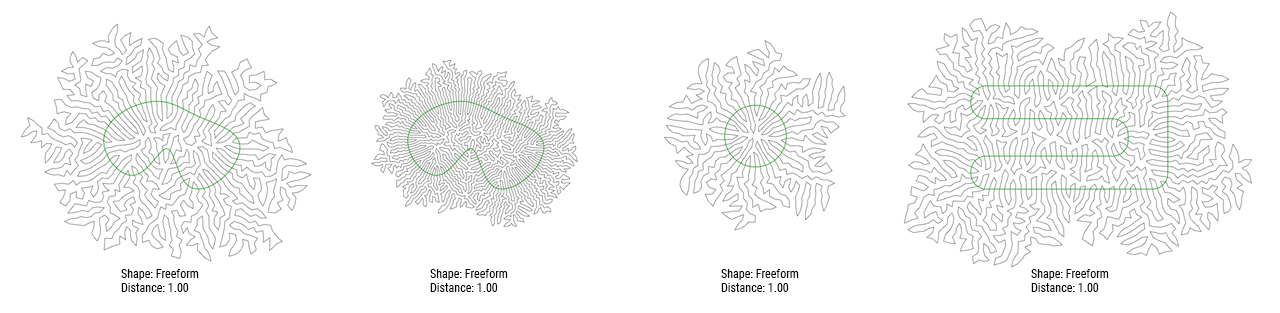
A collection of iterations derived from the example by changing parameters and starting curves
Taking this a step further:
It is possible to add further behaviours top this algorithm to create greater variations of patterns. In our Differential Growth Tutorial, we examine ways to simulate the growth on a surface geometry in Rhino, and add an attractor point for further variation. It is also possible to add further behaviours, such as angle alignments, and point snaps to produce ever greater variation in the geometry output.
